本章全部来自于李航的《统计学》以及他的博客和自己试验。仅供个人复习使用。
Boosting算法通过改变训练样本的权重,学习多个分类器,并将这些分类器进行线性组合,提高分类性能。我们以AdaBoost为例。
它的自适应在于:前一个弱分类器分错的样本的权值(样本对应的权值)会得到加强,权值更新后的样本再次被用来训练下一个新的弱分类器。
在每轮训练中,用总体(样本总体)训练新的弱分类器,产生新的样本权值、该弱分类器的话语权,一直迭代直到达到预定的错误率或达到指定的最大迭代次数。
有两个问题需要回答:
1.每一轮如何改变训练数据的权重或者是概率分布
=>提高那些被前一轮若分类器错误分类样本的权重,而降低那些被正确分类样本的权重值,
so那些没有得到正确分类的数据由于其权重值加大而受到后一轮的弱分类器的更大关注。于是分类问题被一系列的弱分类器“分而治之”
2.如何将如分类器组合成一个强分类器
=>弱分类器的组合,adaboost采取加权多数的表决方法:加大分类误差小的分类器的权值,使其在表决中起较大的作用,减少分类误差率大的弱分类器的权值,使其在变绝种起较小的作用。
那我们总结一下:
(1)初始化训练数据(每个样本)的权值分布:如果有N个样本,则每一个训练的样本点最开始时都被赋予相同的权重:1/N。
(2)训练弱分类器。具体训练过程中,如果某个样本已经被准确地分类,那么在构造下一个训练集中,它的权重就被降低;相反,如果某个样本点没有被准确地分类,那么它的权重就得到提高。
同时,得到弱分类器对应的话语权。然后,更新权值后的样本集被用于训练下一个分类器,整个训练过程如此迭代地进行下去。
(3)将各个训练得到的弱分类器组合成强分类器。各个弱分类器的训练过程结束后,分类误差率小的弱分类器的话语权较大,其在最终的分类函数中起着较大的决定作用,
而分类误差率大的弱分类器的话语权较小,其在最终的分类函数中起着较小的决定作用。换言之,误差率低的弱分类器在最终分类器中占的比例较大,反之较小。



迭代过程1
对于m=1,在权值分布为D1(10个数据,每个数据的权值皆初始化为0.1)的训练数据上,经过计算可得:
阈值v取2.5时误差率为0.3(x < 2.5时取1,x > 2.5时取-1,则6 7 8分错,误差率为0.3),
阈值v取5.5时误差率最低为0.4(x < 5.5时取1,x > 5.5时取-1,则3 4 5 6 7 8皆分错,误差率0.6大于0.5,不可取。故令x > 5.5时取1,x < 5.5时取-1,则0 1 2 9分错,误差率为0.4),阈值v取8.5时误差率为0.3(x < 8.5时取1,x > 8.5时取-1,则3 4 5分错,误差率为0.3)。可以看到,无论阈值v取2.5,还是8.5,总得分错3个样本,故可任取其中任意一个如2.5,弄成第一个基本分类器为: 
上面说阈值v取2.5时则6 7 8分错,所以误差率为0.3,更加详细的解释是:因为样本集中
0 1 2对应的类(Y)是1,因它们本身都小于2.5,所以被G1(x)分在了相应的类“1”中,分对了。
3 4 5本身对应的类(Y)是-1,因它们本身都大于2.5,所以被G1(x)分在了相应的类“-1”中,分对了。但6 7 8本身对应类(Y)是1,却因它们本身大于2.5而被G1(x)分在了类"-1"中,所以这3个样本被分错了。9本身对应的类(Y)是-1,因它本身大于2.5,所以被G1(x)分在了相应的类“-1”中,分对了。从而得到G1(x)在训练数据集上的误差率(被G1(x)误分类样本“6 7 8”的权值之和)e1=P(G1(xi)≠yi) = 3*0.1 = 0.3。然后根据误差率e1计算G1的系数:
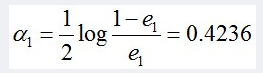
这个a1代表G1(x)在最终的分类函数中所占的权重,为0.4236。
接着更新训练数据的权值分布,用于下一轮迭代: 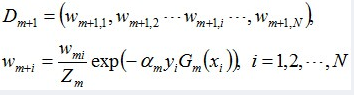
即如果某个样本被分错了,则yi * Gm(xi)为负,负负得正,结果使得整个式子变大(样本权值变大),否则变小。
第一轮迭代后,最后得到各个数据新的权值分布D2 = (0.0715, 0.0715, 0.0715, 0.0715, 0.0715, 0.0715, 0.1666, 0.1666, 0.1666, 0.0715)。由此可以看出,因为样本中是数据“6 7 8”被G1(x)分错了,所以它们的权值由之前的0.1增大到0.1666,反之,其它数据皆被分正确,所以它们的权值皆由之前的0.1减小到0.0715。
分类函数f1(x)= a1*G1(x) = 0.4236G1(x)。
此时,得到的第一个基本分类器sign(f1(x))在训练数据集上有3个误分类点(即6 7 8)。
从上述第一轮的整个迭代过程可以看出:被误分类样本的权值之和影响误差率,误差率影响基本分类器在最终分类器中所占的权重。
迭代过程2
对于m=2,在权值分布为D2 = (0.0715, 0.0715, 0.0715, 0.0715, 0.0715, 0.0715, 0.1666, 0.1666, 0.1666, 0.0715)的训练数据上,经过计算可得:
阈值v取2.5时误差率为0.1666*3(x < 2.5时取1,x > 2.5时取-1,则6 7 8分错,误差率为0.1666*3),
阈值v取5.5时误差率最低为0.0715*4(x > 5.5时取1,x < 5.5时取-1,则0 1 2 9分错,误差率为0.0715*3 + 0.0715),阈值v取8.5时误差率为0.0715*3(x < 8.5时取1,x > 8.5时取-1,则3 4 5分错,误差率为0.0715*3)。所以,阈值v取8.5时误差率最低,故第二个基本分类器为: 
面对的还是下述样本:

很明显,G2(x)把样本“3 4 5”分错了,根据D2可知它们的权值为0.0715, 0.0715, 0.0715,所以G2(x)在训练数据集上的误差率e2=P(G2(xi)≠yi) = 0.0715 * 3 = 0.2143。
计算G2的系数:
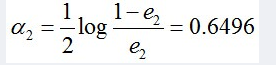
更新训练数据的权值分布:
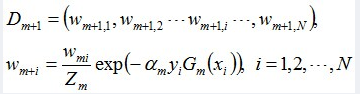
D3 = (0.0455, 0.0455, 0.0455, 0.1667, 0.1667, 0.01667, 0.1060, 0.1060, 0.1060, 0.0455)。被分错的样本“3 4 5”的权值变大,其它被分对的样本的权值变小。
f2(x)=0.4236G1(x) + 0.6496G2(x)
此时,得到的第二个基本分类器sign(f2(x))在训练数据集上有3个误分类点(即3 4 5)。
迭代过程3
对于m=3,在权值分布为D3 = (0.0455, 0.0455, 0.0455, 0.1667, 0.1667, 0.01667, 0.1060, 0.1060, 0.1060, 0.0455)的训练数据上,经过计算可得:
阈值v取2.5时误差率为0.1060*3(x < 2.5时取1,x > 2.5时取-1,则6 7 8分错,误差率为0.1060*3),
阈值v取5.5时误差率最低为0.0455*4(x > 5.5时取1,x < 5.5时取-1,则0 1 2 9分错,误差率为0.0455*3 + 0.0715),阈值v取8.5时误差率为0.1667*3(x < 8.5时取1,x > 8.5时取-1,则3 4 5分错,误差率为0.1667*3)。所以阈值v取5.5时误差率最低,故第三个基本分类器为: 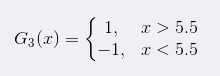
依然还是原样本:

此时,被误分类的样本是:0 1 2 9,这4个样本所对应的权值皆为0.0455,
所以G3(x)在训练数据集上的误差率e3 = P(G3(xi)≠yi) = 0.0455*4 = 0.1820。
计算G3的系数:
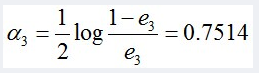
更新训练数据的权值分布:
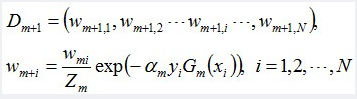
D4 = (0.125, 0.125, 0.125, 0.102, 0.102, 0.102, 0.065, 0.065, 0.065, 0.125)。被分错的样本“0 1 2 9”的权值变大,其它被分对的样本的权值变小。
f3(x)=0.4236G1(x) + 0.6496G2(x)+0.7514G3(x)
此时,得到的第三个基本分类器sign(f3(x))在训练数据集上有0个误分类点。至此,整个训练过程结束。
现在,咱们来总结下3轮迭代下来,各个样本权值和误差率的变化,如下所示(其中,样本权值D中加了下划线的表示在上一轮中被分错的样本的新权值):
训练之前,各个样本的权值被初始化为D1 = (0.1, 0.1,0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1);
第一轮迭代中,样本“6 7 8”被分错,对应的误差率为e1=P(G1(xi)≠yi) = 3*0.1 = 0.3,此第一个基本分类器在最终的分类器中所占的权重为a1 = 0.4236。第一轮迭代过后,样本新的权值为D2 = (0.0715, 0.0715, 0.0715, 0.0715, 0.0715, 0.0715, 0.1666, 0.1666, 0.1666, 0.0715);第二轮迭代中,样本“3 4 5”被分错,对应的误差率为e2=P(G2(xi)≠yi) = 0.0715 * 3 = 0.2143,此第二个基本分类器在最终的分类器中所占的权重为a2 = 0.6496。第二轮迭代过后,样本新的权值为D3 = (0.0455, 0.0455, 0.0455, 0.1667, 0.1667, 0.01667, 0.1060, 0.1060, 0.1060, 0.0455);第三轮迭代中,样本“0 1 2 9”被分错,对应的误差率为e3 = P(G3(xi)≠yi) = 0.0455*4 = 0.1820,此第三个基本分类器在最终的分类器中所占的权重为a3 = 0.7514。第三轮迭代过后,样本新的权值为D4 = (0.125, 0.125, 0.125, 0.102, 0.102, 0.102, 0.065, 0.065, 0.065, 0.125)。 从上述过程中可以发现,如果某些个样本被分错,它们在下一轮迭代中的权值将被增大,同时,其它被分对的样本在下一轮迭代中的权值将被减小。就这样,分错样本权值增大,分对样本权值变小,而在下一轮迭代中,总是选取让误差率最低的阈值来设计基本分类器,所以误差率e(所有被Gm(x)误分类样本的权值之和)不断降低。综上,将上面计算得到的a1、a2、a3各值代入G(x)中,G(x) = sign[f3(x)] = sign[ a1 * G1(x) + a2 * G2(x) + a3 * G3(x) ],得到最终的分类器为:
G(x) = sign[f3(x)] = sign[ 0.4236G1(x) + 0.6496G2(x)+0.7514G3(x) ]。
其实上面还有一点我没有指出就是弱分类器的指定:

弱分类器是提前给出的,或者说是提前训练的。
adaboost中弱分类器的设计还是很重要的:我看了几篇博客和论文以下几点
1任何分类器都行,但要是弱分类器,记得一篇论文中说如果是强分类器会影响最终训练性能,但没有试过。简单点可以用decision stump,其实就是一个判断,如果特征符合某个条件则为a类,否则是b类。其他决策树也行,至于使用不同分类器是不是有很大区别,没有做过实验不敢妄言,但肯定会有性能差别的。
2AdaBoost算法里面 要求弱分类器正确率>50%并且各个弱分类器相互独立 可是如果弱分类器错误率均在50%以下,但不完全独立 会造成什么样的后果呢?,弱分类器用最小平方误差,最小平方误差的错误率应该是50%以下的,可是调整权值会使分类器不独立(也可能不是,因为弱分类器是重新调整权值后重新计算的,跟上一次应该不算线形相关。在AdaBoost算法描述本身,也是用的调整权值来做的 ,说明这样的权值调整,并不会使弱分类器变得相关,不然,AdaBoost算法这么大的漏洞,不可能被广泛应用的),有说会让组合后的分类器错误率>50%而退出~ 可是我觉得不会,迭代算法应该能保证其越来越优,只是可能一直到不了错误率<0附近的值的状态。
3参考博客《》给到很多对弱分类器的设计思考